Note
Go to the end to download the full example code
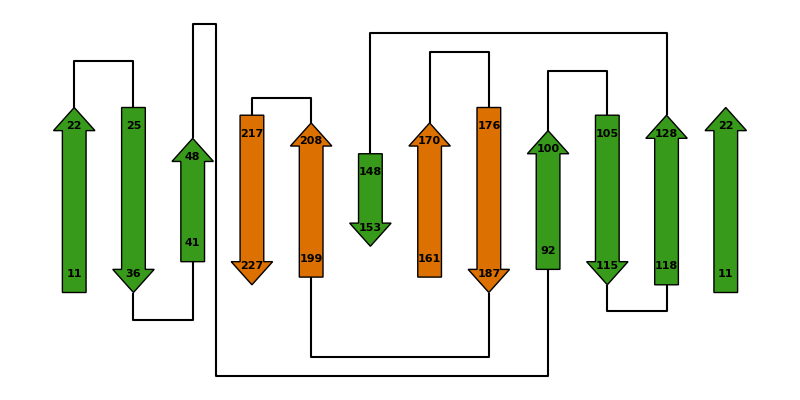
Arrangement of beta-sheets#
This scripts plots the arrangements of strands in selected β-sheets of a
protein structure.
The information is entirely taken from the struct_sheet_order and
struct_sheet_range categories of the corresponding PDBx file
in BinaryCIF format.
In this case the β-barrel of a split fluorescent protein is shown, but the script can be customized to show the β-sheets of any protein you like. You just need to adjust the options shown below.
# Code source: Patrick Kunzmann
# License: BSD 3 clause
import matplotlib.pyplot as plt
import networkx as nx
import numpy as np
from matplotlib.patches import FancyArrow
import biotite
import biotite.database.rcsb as rcsb
import biotite.structure.io.pdbx as pdbx
##### OPTIONS #####
PDB_ID = "3AKO"
SHEETS = ["A"]
FIG_SIZE = (8.0, 4.0) # Figure size in inches
Y_LIMIT = 2.0 # Vertical plot limits
SHEET_DISTANCE = 3.0 # Separation of strands in different sheets
ARROW_TAIL_WITH = 0.4 # Width of the arrow tails
ARROW_HEAD_WITH = 0.7 # Width of the arrow heads
ARROW_HEAD_LENGTH = 0.25 # Length of the arrow heads
ARROW_LINE_WIDTH = 1 # Width of the arrow edges
ARROW_COLORS = [ # Each chain is colored differently
biotite.colors["darkgreen"],
biotite.colors["dimorange"],
biotite.colors["lightgreen"],
biotite.colors["brightorange"],
]
CONNECTION_COLOR = "black" # Color of the connection lines
CONNECTION_LINE_WIDTH = 1.5 # Width of the connection lines
CONNECTION_HEIGHT = 0.1 # Minimum height of the connection lines
CONNECTION_SEPARATION = 0.1 # Minimum vertical distance between the connection lines
RES_ID_HEIGHT = (
-0.2
) # The vertical distance of the residue ID labels from the arrow ends
RES_ID_FONT_SIZE = 8 # The font size of the residue ID labels
RES_ID_FONT_WEIGHT = "bold" # The font weight of the residue ID labels
ADAPTIVE_ARROW_LENGTHS = (
True # If true, the arrow length is proportional to the number of its residues
)
SHOW_SHEET_NAMES = False # If true, the sheets are labeled below the plot
SHEET_NAME_FONT_SIZE = 14 # The font size of the sheet labels
##### SNOITPO #####
The struct_sheet_order category of the BinaryCIF file gives us
the information about the existing sheets, the strands these sheets
contain and which of these strands are connected with one another
in either parallel or anti-parallel orientation.
We can use this to select only strands that belong to those sheets, we are interested in. The strand adjacency and relative orientation is also saved for later.
bcif_file = pdbx.BinaryCIFFile.read(rcsb.fetch(PDB_ID, "bcif"))
sheet_order = bcif_file.block["struct_sheet_order"]
# Create a boolean mask that covers the selected sheets
# or all sheets if none is given
if SHEETS is None:
sele = np.full(sheet_order.row_count, True)
else:
sele = np.array([sheet in SHEETS for sheet in sheet_order["sheet_id"].as_array()])
sheet_ids = sheet_order["sheet_id"].as_array()[sele]
is_parallel_list = sheet_order["sense"].as_array()[sele] == "parallel"
adjacent_strands = np.array(
[
(strand_i, strand_j)
for strand_i, strand_j in zip(
sheet_order["range_id_1"].as_array()[sele],
sheet_order["range_id_2"].as_array()[sele],
)
]
)
print("Adjacent strands (sheet ID, strand ID):")
for sheet_id, (strand_i, strand_j) in zip(sheet_ids, adjacent_strands):
print(f"{sheet_id, strand_i} <-> {sheet_id, strand_j}")
Adjacent strands (sheet ID, strand ID):
(np.str_('A'), np.int32(1)) <-> (np.str_('A'), np.int32(2))
(np.str_('A'), np.int32(2)) <-> (np.str_('A'), np.int32(3))
(np.str_('A'), np.int32(3)) <-> (np.str_('A'), np.int32(4))
(np.str_('A'), np.int32(4)) <-> (np.str_('A'), np.int32(5))
(np.str_('A'), np.int32(5)) <-> (np.str_('A'), np.int32(6))
(np.str_('A'), np.int32(6)) <-> (np.str_('A'), np.int32(7))
(np.str_('A'), np.int32(7)) <-> (np.str_('A'), np.int32(8))
(np.str_('A'), np.int32(8)) <-> (np.str_('A'), np.int32(9))
(np.str_('A'), np.int32(9)) <-> (np.str_('A'), np.int32(10))
(np.str_('A'), np.int32(10)) <-> (np.str_('A'), np.int32(11))
(np.str_('A'), np.int32(11)) <-> (np.str_('A'), np.int32(12))
The struct_sheet_range category of the mmCIF file tells us
which residues compose each strand in terms of chain and
residue IDs.
Later the plot shall display connections between consecutive strands in a protein chain. Although, this category does not provide this connection information directly, we can sort the strands by their beginning chain and residue IDs and then simply connect successive entries.
sheet_range = bcif_file.block["struct_sheet_range"]
# Again, create a boolean mask that covers the selected sheets
sele = np.array([sheet in sheet_ids for sheet in sheet_range["sheet_id"].as_array()])
strand_chain_ids = sheet_range["beg_auth_asym_id"].as_array()[sele]
strand_res_id_begs = sheet_range["beg_auth_seq_id"].as_array(int)[sele]
strand_res_id_ends = sheet_range["end_auth_seq_id"].as_array(int)[sele]
# Secondarily sort by residue ID
order = np.argsort(strand_res_id_begs, kind="stable")
# Primarily sort by chain ID
order = order[np.argsort(strand_chain_ids[order], kind="stable")]
sorted_strand_ids = sheet_range["id"].as_array()[sele][order]
sorted_sheet_ids = sheet_range["sheet_id"].as_array()[sele][order]
sorted_chain_ids = strand_chain_ids[order]
sorted_res_id_begs = strand_res_id_begs[order]
sorted_res_id_ends = strand_res_id_ends[order]
# Remove duplicate entries,
# i.e. entries with the same chain ID and residue ID
# Duplicate entries appear e.g. in beta-barrel structure files
# Draw one of each duplicate as orphan -> no connections
non_duplicate_mask = np.diff(strand_res_id_begs[order], prepend=[-1]) != 0
connections = []
non_duplicate_indices = np.arange(len(sorted_strand_ids))[non_duplicate_mask]
for i in range(len(non_duplicate_indices) - 1):
current_i = non_duplicate_indices[i]
next_i = non_duplicate_indices[i + 1]
if sorted_chain_ids[current_i] != sorted_chain_ids[next_i]:
# No connection between separate chains
continue
connections.append(
(
(sorted_sheet_ids[current_i], sorted_strand_ids[current_i]),
(sorted_sheet_ids[next_i], sorted_strand_ids[next_i]),
)
)
print("Connected strands (sheet ID, strand ID):")
for strand_i, strand_j in connections:
print(f"{strand_i} -> {strand_j}")
# Save the start and end residue IDs for each strand for labeling
ranges = {
(sheet_id, strand_id): (begin, end)
for sheet_id, strand_id, begin, end in zip(
sorted_sheet_ids, sorted_strand_ids, sorted_res_id_begs, sorted_res_id_ends
)
}
# Save the chains ID for each strand for coloring
chain_ids = {
(sheet_id, strand_id): chain_id
for sheet_id, strand_id, chain_id in zip(
sorted_sheet_ids, sorted_strand_ids, sorted_chain_ids
)
}
unique_chain_ids = np.unique(sorted_chain_ids)
Connected strands (sheet ID, strand ID):
(np.str_('A'), np.int32(1)) -> (np.str_('A'), np.int32(2))
(np.str_('A'), np.int32(2)) -> (np.str_('A'), np.int32(3))
(np.str_('A'), np.int32(3)) -> (np.str_('A'), np.int32(9))
(np.str_('A'), np.int32(9)) -> (np.str_('A'), np.int32(10))
(np.str_('A'), np.int32(10)) -> (np.str_('A'), np.int32(11))
(np.str_('A'), np.int32(11)) -> (np.str_('A'), np.int32(6))
(np.str_('A'), np.int32(7)) -> (np.str_('A'), np.int32(8))
(np.str_('A'), np.int32(8)) -> (np.str_('A'), np.int32(5))
(np.str_('A'), np.int32(5)) -> (np.str_('A'), np.int32(4))
So far we only know which strands to plot adjacent to each other, but we still need to determine the position in the plot for each strand. For this purpose we will later use one of NetworkX’s layouting algorithms. For now the information about the adjacent strands is stored in a NetworkX graph, one for each sheet: The strand IDs are nodes and the adjacency is represented by edges. The relative strand orientation is stored as edge attribute.
sheet_graphs = {}
for sheet_id in np.unique(sheet_ids):
# Select only strands from the current sheet
sheet_mask = sheet_ids == sheet_id
sheet_graphs[sheet_id] = nx.Graph(
[
(strand_i, strand_j, {"is_parallel": is_parallel})
for (strand_i, strand_j), is_parallel in zip(
adjacent_strands[sheet_mask], is_parallel_list[sheet_mask]
)
]
)
Another missing information is the direction of the plotted arrows, we only know their relative orientations. To solve this, we initially let the arrow for the first strand of each sheet point upwards and then iteratively determine the direction of the other arrows from the relative orientations.
For example, strand '1' is set to point upward, strand '2'
is anti-parallel to strand '1', so it points downward, strand
'3' is parallel to strand '2' so it points also downward.
The calculated arrow direction is stored as node attribute.
for graph in sheet_graphs.values():
initial_strand = adjacent_strands[0, 0]
graph.nodes[initial_strand]["is_upwards"] = True
for strand in graph.nodes:
if strand == initial_strand:
continue
this_strand_is_upwards = []
for adj_strand in graph.neighbors(strand):
is_upwards = graph.nodes[adj_strand].get("is_upwards")
if is_upwards is None:
# The arrow direction for this adjacent strand is not
# yet determined
continue
is_parallel = graph.edges[(strand, adj_strand)]["is_parallel"]
this_strand_is_upwards.append(is_upwards ^ ~is_parallel)
if len(this_strand_is_upwards) == 0:
raise ValueError("Cannot determine arrow direction from adjacent strands")
elif all(this_strand_is_upwards):
graph.nodes[strand]["is_upwards"] = True
elif not any(this_strand_is_upwards):
graph.nodes[strand]["is_upwards"] = False
else:
raise ValueError("Conflicting arrow directions from adjacent strands")
No we have got all positioning information we need to start plotting.
fig, ax = plt.subplots(figsize=FIG_SIZE)
### Plot arrows
MAX_ARROW_LENGTH = 2 # from y=-1 to y=1
arrow_length_per_seq_length = MAX_ARROW_LENGTH / np.max(
[end - beg + 1 for beg, end in ranges.values()]
)
# The coordinates of the arrow ends are stored in this dictionary
# for each strand, accessed via a tuple of sheet and strand ID
coord_dict = {}
current_position = 0
# Plot each sheet separately,
# the start position of each sheet is given by 'current_position'
for sheet_id, graph in sheet_graphs.items():
# Use *NetworkX*'s layouting algorithm to find the arrow positions
# As we arrange the sheets along the x-axis,
# there is only one dimension
positions = nx.kamada_kawai_layout(graph, dim=1)
strand_ids = np.array(list(positions.keys()))
positions = np.array(list(positions.values()))
# Each position has only one dimension
# -> Remove the last dimension
positions = positions[:, 0]
# Transform positions to achieve a spacing of at least 1.0
dist_matrix = np.abs(positions[:, np.newaxis] - positions[np.newaxis, :])
positions /= np.min(dist_matrix[dist_matrix != 0])
# Transform positions, so that they start at 'current_position'
positions -= np.min(positions)
positions += np.min(current_position)
current_position = np.max(positions) + SHEET_DISTANCE
# Draw an arrow for each strand
for strand_id, pos in zip(strand_ids, positions):
chain_id = chain_ids[sheet_id, strand_id]
color_index = unique_chain_ids.tolist().index(chain_id)
if ADAPTIVE_ARROW_LENGTHS:
beg, end = ranges[sheet_id, strand_id]
seq_length = end - beg + 1
arrow_length = arrow_length_per_seq_length * seq_length
else:
arrow_length = MAX_ARROW_LENGTH
if graph.nodes[strand_id]["is_upwards"]:
y = -arrow_length / 2
dy = arrow_length
else:
y = arrow_length / 2
dy = -arrow_length
ax.add_patch(
FancyArrow(
x=pos,
y=y,
dx=0,
dy=dy,
length_includes_head=True,
width=ARROW_TAIL_WITH,
head_width=ARROW_HEAD_WITH,
head_length=ARROW_HEAD_LENGTH,
facecolor=ARROW_COLORS[color_index % len(ARROW_COLORS)],
edgecolor=CONNECTION_COLOR,
linewidth=ARROW_LINE_WIDTH,
)
)
# Start and end coordinates of the respective arrow
coord_dict[sheet_id, strand_id] = ((pos, y), (pos, y + dy))
### Plot connections
# Each connection is plotted on a different height in order to keep them
# separable
# Plot the short connections at low height
# to decrease line intersections
# -> sort connections by length of connection
order = np.argsort(
[
np.abs(coord_dict[strand_i][0][0] - coord_dict[strand_j][0][0])
for strand_i, strand_j in connections
]
)
connections = [connections[i] for i in order]
for i, (strand_i, strand_j) in enumerate(connections):
horizontal_line_height = 1 + CONNECTION_HEIGHT + i * CONNECTION_SEPARATION
coord_i_beg, coord_i_end = coord_dict[strand_i]
coord_j_beg, coord_j_end = coord_dict[strand_j]
if np.sign(coord_i_end[1]) == np.sign(coord_j_beg[1]):
# Start and end are on the same side of the arrows
x = (coord_i_end[0], coord_i_end[0], coord_j_beg[0], coord_j_beg[0])
y = (
coord_i_end[1],
np.sign(coord_i_end[1]) * horizontal_line_height,
np.sign(coord_j_beg[1]) * horizontal_line_height,
coord_j_beg[1],
)
else:
# Start and end are on different sides
offset = 0.4 if coord_j_beg[0] >= coord_i_end[0] else -0.4
x = (
coord_i_end[0],
coord_i_end[0],
coord_i_end[0] + offset,
coord_i_end[0] + offset,
coord_j_beg[0],
coord_j_beg[0],
)
y = (
coord_i_end[1],
np.sign(coord_i_end[1]) * horizontal_line_height,
np.sign(coord_i_end[1]) * horizontal_line_height,
np.sign(coord_j_beg[1]) * horizontal_line_height,
np.sign(coord_j_beg[1]) * horizontal_line_height,
coord_j_beg[1],
)
ax.plot(
x,
y,
color=CONNECTION_COLOR,
linewidth=CONNECTION_LINE_WIDTH,
# Avoid intersection of the line's end with the arrow
solid_capstyle="butt",
)
### Plot residue ID labels
for strand, (res_id_beg, res_id_end) in ranges.items():
coord_beg, coord_end = coord_dict[strand]
for coord, res_id in zip((coord_beg, coord_end), (res_id_beg, res_id_end)):
ax.text(
coord[0],
np.sign(coord[1]) * (np.abs(coord[1]) + RES_ID_HEIGHT),
str(res_id),
ha="center",
va="center",
fontsize=RES_ID_FONT_SIZE,
weight=RES_ID_FONT_WEIGHT,
)
### Plot sheet names as x-axis ticks
if SHOW_SHEET_NAMES:
tick_pos = [
np.mean([coord_dict[key][0][0] for key in coord_dict if key[0] == sheet_id])
for sheet_id in sheet_ids
]
ax.set_xticks(tick_pos)
ax.set_xticklabels([f"Sheet {sheet_id}" for sheet_id in sheet_ids])
ax.set_frame_on(False)
ax.yaxis.set_visible(False)
ax.xaxis.set_tick_params(
bottom=False,
top=False,
labelbottom=True,
labeltop=False,
labelsize=SHEET_NAME_FONT_SIZE,
)
else:
ax.axis("off")
ax.set_xlim(-1, current_position - SHEET_DISTANCE + 1)
ax.set_ylim(-Y_LIMIT, Y_LIMIT)
fig.tight_layout()
plt.show()